Qué son las ecuaciones de primer año de secundaria y cómo se resuelven

✅ Las ecuaciones de primer año son expresiones matemáticas simples con una incógnita (x). Se resuelven despejando x mediante operaciones básicas.

Las ecuaciones de primer año de secundaria son expresiones matemáticas que establecen una igualdad entre dos cantidades, donde al menos una de las cantidades contiene una variable. Estas ecuaciones se representan generalmente en la forma ax + b = c, donde a, b y c son números reales y x es la variable que queremos resolver.

Exploraremos en detalle qué son las ecuaciones de primer año de secundaria, cómo se clasifican y los pasos necesarios para resolverlas. Aprender a solucionar ecuaciones es fundamental no solo en matemáticas, sino también en diversas áreas de la vida cotidiana, ya que nos ayuda a desarrollar habilidades de razonamiento lógico y pensamiento crítico.

Características de las ecuaciones

Las ecuaciones de primer año de secundaria presentan varias características importantes que son clave para su comprensión y resolución:

• Variables: Representan cantidades desconocidas y se suelen denotar con letras, como x y y.
• Constantes: Son los números que acompañan a las variables en la ecuación.
• Igualdad: La presencia del signo igual (=) indica que ambas partes de la ecuación son equivalentes.

Tipos de ecuaciones de primer año

Existen diferentes tipos de ecuaciones que se enseñan en primer año de secundaria:

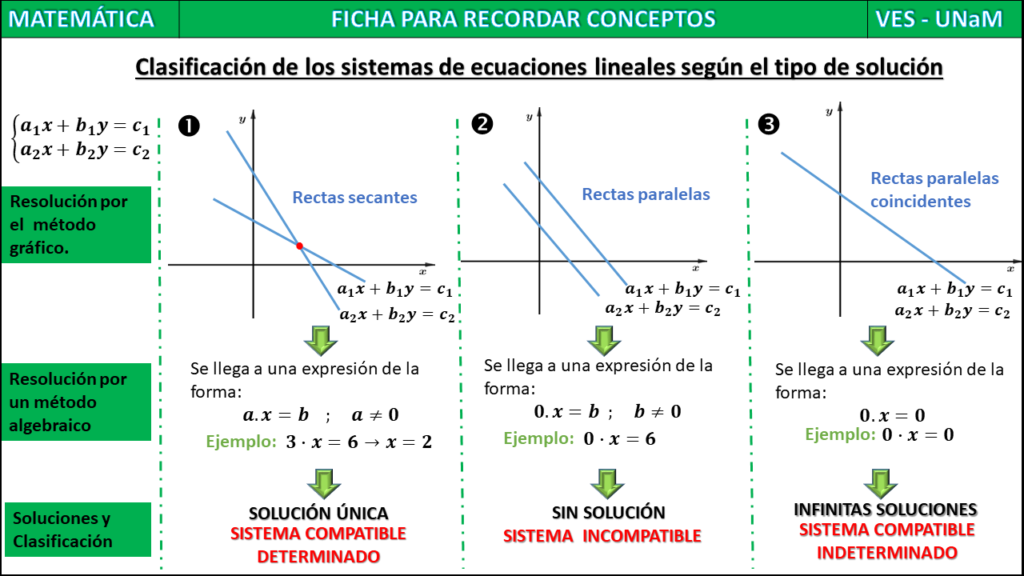
1. Ecuaciones lineales: Son aquellas que se pueden representar en la forma ax + b = c.
2. Ecuaciones con una solución: Tienen un único valor de x que satisface la igualdad.
3. Ecuaciones sin solución: No existen valores que hagan verdadera la igualdad.
4. Ecuaciones con infinitas soluciones: Son aquellas donde cualquier valor de x satisface la ecuación.

Pasos para resolver ecuaciones

Resolver ecuaciones implica seguir una serie de pasos que aseguran que se manipulan correctamente los términos. A continuación, se presentan los pasos básicos:

1. Aislar la variable: Reorganizar la ecuación para que la variable quede sola en un lado.
2. Realizar operaciones inversas: Aplicar operaciones que deshagan los efectos de las constantes que acompañan a la variable.
3. Verificar la solución: Sustituir el valor encontrado en la ecuación original para asegurarse de que ambas partes son iguales.

Ejemplo práctico

Consideremos la ecuación 2x + 3 = 11. Para resolverla, seguimos estos pasos:

• Restamos 3 de ambos lados: 2x = 8.
• Dividimos ambos lados por 2: x = 4.
• Verificamos sustituyendo en la ecuación original: 2(4) + 3 = 11, lo cual es verdadero.

Importancia de las ecuaciones en la vida cotidiana y el pensamiento lógico

Las ecuaciones no son solo una parte de las matemáticas que se estudian en la escuela; también juegan un papel fundamental en nuestra vida cotidiana. Desde calcular el costo de una compra hasta planificar un viaje, las ecuaciones nos ayudan a resolver problemas y tomar decisiones informadas.

Ejemplos de uso cotidiano de las ecuaciones

• Finanzas personales: Supongamos que quieres saber cuánto dinero te queda después de hacer una compra. Si tienes $100 y compras algo que cuesta $30, puedes usar la ecuación: x = 100 – 30, donde x representa el dinero que te queda.
• Planificación de recetas: Si una receta sirve para 4 personas y quieres cocinar para 10, puedes establecer una ecuación para ajustar los ingredientes. Por ejemplo, si necesitas 2 kg de pollo para 4 personas, ¿cuánto necesitas para 10? La relación puede expresarse como: x = (10/4) * 2.
• Viajes y distancias: Si viajas a una velocidad promedio de 60 km/h y quieres saber cuántas horas tardarás en llegar a un destino que está a 180 km, puedes usar la ecuación: x = 180/60, donde x es el tiempo en horas.

Desarrollo del pensamiento lógico

Además de su utilidad práctica, las ecuaciones son esenciales para desarrollar el pensamiento lógico. Resolver ecuaciones implica seguir un proceso estructurado que mejora la capacidad de análisis y razonamiento. Esto no solo es beneficioso en matemáticas, sino que también es aplicable en otras áreas como la física, la ingeniería y la programación.

Beneficios de aprender a resolver ecuaciones

1. Mejora en la resolución de problemas: Aprender a manejar ecuaciones permite a los estudiantes abordar problemas complejos de manera más eficiente.
2. Desarrollo de habilidades analíticas: La práctica constante de resolver ecuaciones refuerza la capacidad de analizar información y tomar decisiones basadas en datos.
3. Preparación para estudios futuros: Las ecuaciones son la base de muchos temas avanzados en matemáticas y ciencias, lo que las convierte en una herramienta crucial para el éxito académico.

Estadísticas que respaldan la importancia de las ecuaciones

Un estudio del Departamento de Educación revela que los estudiantes que dominan la resolución de ecuaciones tienen un 20% más de probabilidades de calificar en los niveles más altos de matemáticas en su educación secundaria. Esto demuestra que un buen dominio de las ecuaciones puede tener un impacto significativo en el rendimiento académico general.

Entender e identificar la importancia de las ecuaciones en la vida diaria y el desarrollo de habilidades lógicas no solo es esencial para el éxito en las matemáticas, sino que también tiene un efecto duradero en la toma de decisiones en diversas áreas de la vida.

Preguntas frecuentes

¿Qué es una ecuación de primer año de secundaria?

Es una igualdad matemática que incluye una o más incógnitas, que se resuelve para encontrar los valores de estas incógnitas.

¿Cómo se identifica una ecuación?

Una ecuación se identifica por tener un signo igual (=) y variables que deben ser despejadas.

¿Qué tipos de ecuaciones se ven en primer año?

Principalmente se trabajan ecuaciones lineales, que son de la forma ax + b = 0.

¿Cuál es el primer paso para resolver una ecuación?

El primer paso es aislar la variable en uno de los lados de la ecuación.

¿Qué se hace si la ecuación tiene fracciones?

Se puede multiplicar toda la ecuación por el mínimo común múltiplo para eliminar las fracciones.

¿Es importante comprobar la solución?

Sí, siempre es recomendable sustituir la solución de vuelta en la ecuación original para verificar que sea correcta.

Puntos clave sobre las ecuaciones de primer año de secundaria

• Definición: Igualdad con incógnitas.
• Forma general: ax + b = 0.
• Pasos para resolver:
  • Aislar la variable.
  • Eliminar fracciones si es necesario.
  • Realizar operaciones inversas.
• Comprobación de soluciones.
• Aplicaciones: Resolución de problemas cotidianos.

¡Dejanos tus comentarios!

Nos encantaría saber qué piensas sobre el tema. No olvides revisar otros artículos de nuestra web que también podrían interesarte.