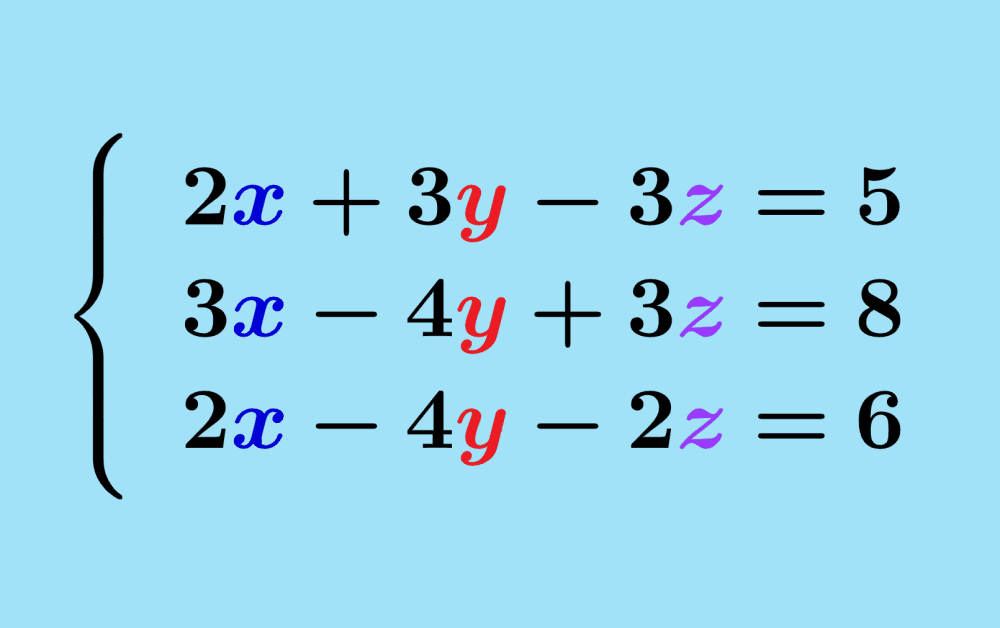✅ Para resolver ecuaciones algebraicas con múltiples variables «x», utiliza métodos como sustitución, igualación o reducción para simplificar y encontrar las soluciones.
Resolver ecuaciones algebraicas con más de una x puede parecer complicado, pero con el enfoque adecuado se puede hacer de manera sencilla y efectiva. El primer paso es identificar todas las x presentes en la ecuación y determinar sus relaciones. Esto involucra simplificar la ecuación, agrupar términos similares y, en muchos casos, aplicar operaciones inversas para despejar la variable.
Exploraremos el proceso paso a paso para resolver ecuaciones algebraicas que contienen más de una x. Para facilitar la comprensión, utilizaremos ejemplos y métodos que son fáciles de seguir. Además, proporcionaremos consejos y técnicas que te ayudarán a evitar errores comunes al manejar este tipo de ecuaciones.
Pasos para resolver ecuaciones con más de una x
1. Simplificación de la ecuación
El primer paso es simplificar la ecuación. Esto incluye eliminar paréntesis, combinar términos semejantes y asegurarse de que todas las x estén del mismo lado de la ecuación. Un ejemplo de esto sería:
Ejemplo: 2(x + 1) + 3x = 15
Primero, distribuimos el 2:
2x + 2 + 3x = 15
Luego, combinamos términos semejantes:
5x + 2 = 15
2. Aislar la variable
Una vez que tenemos todos los términos con x en un lado, el siguiente paso es aislar la variable. Esto se hace restando o sumando términos constantes a ambos lados de la ecuación:
5x = 15 - 2 5x = 13
Finalmente, dividimos ambos lados por 5 para despejar x:
x = 13/5
3. Comprobar la solución
Siempre es recomendable comprobar la solución obtenida. Sustituyendo el valor de x en la ecuación original:
2((13/5) + 1) + 3(13/5) = 15
Realizando la comprobación, vemos que ambos lados de la ecuación son iguales, lo que confirma que x = 13/5 es la solución correcta.
Consejos para resolver ecuaciones con más de una x
- Organización: Mantén un registro claro de tus pasos. Puede ser útil escribir cada paso en una hoja separada.
- Revisar errores: Verifica cada operación realizada para evitar errores de cálculo.
- Practicar: Cuanto más practiques, más cómodo te sentirás resolviendo ecuaciones con múltiples variables.
Resolver ecuaciones algebraicas con más de una x requiere paciencia y práctica, pero siguiendo estos pasos y consejos, cualquier estudiante puede dominar el tema. A lo largo de este artículo, veremos más ejemplos y diferentes tipos de ecuaciones que pueden surgir, así como estrategias adicionales para manejarlas eficazmente.
Pasos detallados para simplificar ecuaciones con múltiples incógnitas
Resolver ecuaciones algebraicas con más de una x puede parecer complicado al principio, pero siguiendo algunos pasos detallados, es posible simplificarlas y encontrar la solución. A continuación, se presentan los pasos que debes seguir:
Paso 1: Identificar la ecuación
El primer paso es identificar la ecuación que deseas resolver. Asegúrate de que todas las incógnitas estén claramente visibles. Por ejemplo:
- 2x + 3y = 12
- 4x – y = 5
Paso 2: Agrupar términos semejantes
En este paso, agrupa los términos semejantes. Esto significa que debes juntar todas las x y todas las y en un mismo lado de la ecuación. Por ejemplo:
- Reescribe 2x + 3y = 12 como 2x = 12 – 3y
- Reescribe 4x – y = 5 como 4x = 5 + y
Paso 3: Aislar una de las incógnitas
Ahora, aisla una de las incógnitas. Esto puede implicar despejar una variable. Por ejemplo, a partir de la ecuación 2x = 12 – 3y:
- x = (12 – 3y) / 2
Paso 4: Sustituir la incógnita aislada
Una vez que has aislado una variable, sustitúyela en la otra ecuación para encontrar el valor de la otra incógnita. Por ejemplo, si sustituyes x en la ecuación 4x – y = 5:
- 4((12 – 3y) / 2) – y = 5
Esto se puede simplificar a:
- 24 – 6y – y = 5
- 24 – 7y = 5
Paso 5: Resolver la ecuación resultante
A partir de aquí, resuelve la ecuación que obtuviste. En este caso,:
- -7y = 5 – 24
- -7y = -19
- y = 19/7
Paso 6: Sustituir para encontrar la otra incógnita
Finalmente, sustituye el valor encontrado de y en la ecuación que habías utilizado para despejar x:
- x = (12 – 3(19/7)) / 2
Realiza las operaciones necesarias para obtener el valor de x.
Consejos prácticos
- Siempre simplifica: Reduce las fracciones y agrupa términos antes de proceder a resolver la ecuación.
- Verifica tus resultados: Una vez que obtengas los valores de x y y, verifica que estos satisfacen ambas ecuaciones originales.
- Utiliza gráficos: En algunos casos, graficar las ecuaciones puede facilitar la comprensión de las intersecciones y soluciones.
Ejemplo de caso práctico
Supongamos que en una encuesta se encontró que 70 personas prefieren el chocolate y 50 prefieren la vainilla, de un total de 100 personas. Si x es el número de personas que prefieren el chocolate y y el de vainilla, entonces podemos plantear:
- x + y = 100
- 2x + y = 120
Siguiendo los pasos anteriores, podemos resolver estas ecuaciones y encontrar el número de personas que prefieren cada sabor.
Preguntas frecuentes
¿Qué son las ecuaciones algebraicas?
Las ecuaciones algebraicas son igualdades que contienen al menos una variable, representando relaciones matemáticas.
¿Cómo se resuelven ecuaciones con más de una x?
Se pueden resolver agrupando términos similares, aplicando operaciones inversas y simplificando la ecuación.
¿Qué métodos existen para resolver estas ecuaciones?
Los métodos más comunes son la factorización, sustitución y el uso de fórmulas algebraicas.
¿Qué hacer si la ecuación es complicada?
Cuando la ecuación es compleja, se recomienda descomponerla en partes más simples o usar herramientas tecnológicas.
¿Es necesario conocer la factorización para resolver ecuaciones?
Sí, la factorización es una técnica fundamental que facilita la resolución de muchas ecuaciones algebraicas.
¿Puedo usar calculadoras para resolver ecuaciones?
Por supuesto, las calculadoras pueden ayudar a verificar resultados y resolver ecuaciones más rápidamente.
Puntos clave sobre la resolución de ecuaciones algebraicas
- Identificar términos similares.
- Aplicar operaciones inversas para despejar variables.
- Utilizar la propiedad distributiva si es necesario.
- Factorizar para simplificar ecuaciones complejas.
- Verificar cada solución sustituyéndola en la ecuación original.
- Practicar con diferentes tipos de ecuaciones para afianzar conocimientos.
¡Déjanos tus comentarios sobre tus dudas y experiencias resolviendo ecuaciones! No olvides revisar otros artículos de nuestra web que también te pueden interesar.