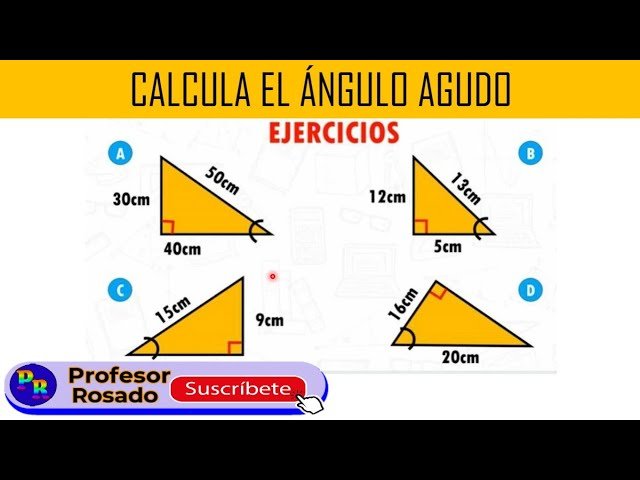
✅ Los ángulos interiores de un triángulo siempre suman 180°. Para calcularlos, resta los ángulos conocidos de 180°. ¡Matemática simple y esencial!
Los ángulos interiores de un triángulo son las medidas angulares que se forman en el interior de la figura triangular por la intersección de sus lados. La suma de estos ángulos siempre es igual a 180 grados, independientemente del tipo de triángulo que se esté considerando (escálenos, isósceles o equilátero).
Para calcular los ángulos interiores de un triángulo, se pueden utilizar diferentes métodos, dependiendo de la información disponible. Si se conocen las longitudes de los lados, se puede aplicar la ley de los cosenos o la ley de los senos. En caso de que se tengan dos ángulos y un lado, se puede aplicar la ley de los ángulos para determinar el tercer ángulo.
Métodos de cálculo de los ángulos interiores
1. Ley de los senos
La ley de los senos establece que la razón entre la longitud de un lado de un triángulo y el seno del ángulo opuesto es constante. Se expresa de la siguiente manera:
a/sen(A) = b/sen(B) = c/sen(C)Donde «a», «b» y «c» son las longitudes de los lados del triángulo y «A», «B» y «C» son los ángulos opuestos a estos lados. Con esta información, si conoces la longitud de al menos un lado y su ángulo opuesto, puedes despejar y encontrar los demás ángulos.
2. Ley de los cosenos
La ley de los cosenos es útil para encontrar un ángulo cuando se conocen los tres lados del triángulo. Se expresa de la siguiente forma:
C^2 = A^2 + B^2 - 2AB*cos(C)Donde «C» es el lado opuesto al ángulo que queremos calcular, y «A» y «B» son los otros dos lados. Al despejar «C» se puede calcular el ángulo correspondiente usando la función inversa del coseno.
3. Cálculo con dos ángulos conocidos
Si ya conoces dos ángulos de un triángulo, el tercer ángulo se puede calcular con una simple resta:
C = 180 - (A + B)Esto es muy útil en triángulos isósceles, donde dos ángulos son iguales.
Ejemplo práctico
Supongamos que tienes un triángulo con lados de longitud a = 7, b = 9, y c = 10. Para calcular el ángulo A, puedes aplicar la ley de los cosenos:
A = cos-1((b^2 + c^2 - a^2) / (2bc))Al sustituir los valores:
A = cos-1((9^2 + 10^2 - 7^2) / (2 * 9 * 10))Esto te permitirá determinar el valor del ángulo A, y luego puedes repetir el proceso para los otros ángulos.
Propiedades fundamentales de los ángulos interiores en un triángulo
Los ángulos interiores de un triángulo son elementos clave que nos ayudan a entender mejor la geometría y la matemática en general. Cada triángulo, sin importar su tipo, posee propiedades específicas que son esenciales para su análisis. A continuación, exploraremos estas propiedades.
1. Suma de los ángulos interiores
Una de las propiedades más importantes de los ángulos interiores de un triángulo es que su suma siempre es igual a 180 grados. Esto significa que si conoces dos de los ángulos, puedes encontrar el tercero restando la suma de los ángulos conocidos de 180. Por ejemplo:
- Si un triángulo tiene ángulos de 50 y 60 grados, el tercer ángulo se calcula como: 180 – (50 + 60) = 70 grados.
- Si un triángulo tiene ángulos de 30 y 90 grados, el tercer ángulo será: 180 – (30 + 90) = 60 grados.
2. Tipos de triángulos según sus ángulos
Los triángulos se pueden clasificar según la medida de sus ángulos interiores:
- Triángulo acutángulo: Tiene todos sus ángulos menores de 90 grados.
- Triángulo rectángulo: Posee un ángulo recto (90 grados).
- Triángulo obtusángulo: Uno de sus ángulos es mayor de 90 grados.
3. Relación con los ángulos exteriores
Los ángulos exteriores de un triángulo se forman al extender uno de sus lados. La relación entre los ángulos interiores y exteriores es fundamental:
- El ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes. Por ejemplo, si un triángulo tiene ángulos interiores de 50 y 60 grados, el ángulo exterior correspondiente al ángulo de 60 grados será: 50 + 60 = 110 grados.
4. Propiedades adicionales
Algunas otras propiedades relevantes incluyen:
- Los ángulos opuestos en un triángulo son siempre congruentes en triángulos isósceles.
- En un triángulo equilátero, todos los ángulos son iguales y miden 60 grados.
Conocer estas propiedades es fundamental para resolver problemas relacionados con triángulos y es un paso inicial en el estudio de la geometría. A medida que profundicemos en el tema, se abrirán nuevas puertas para explorar conceptos más avanzados y su aplicación en situaciones prácticas.
Preguntas frecuentes
¿Cuáles son los ángulos interiores de un triángulo?
Los ángulos interiores de un triángulo son los ángulos que se encuentran dentro del triángulo, y la suma de ellos siempre es 180 grados.
¿Cómo se calcula un ángulo interior si conozco los otros dos?
Para calcular un ángulo interior, simplemente resta la suma de los otros dos ángulos de 180 grados.
¿Qué tipo de triángulo tiene ángulos iguales?
Un triángulo equilátero tiene todos sus ángulos interiores iguales, cada uno mide 60 grados.
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es aquel que tiene un ángulo interior de 90 grados y los otros dos ángulos suman 90 grados.
¿Cómo se relacionan los ángulos interiores con el teorema de Pitágoras?
El teorema de Pitágoras se aplica en triángulos rectángulos, donde la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Puntos clave sobre los ángulos interiores de un triángulo
- Suma de ángulos interiores = 180 grados.
- Triángulo equilátero: 3 ángulos de 60 grados.
- Triángulo isósceles: 2 ángulos iguales y 1 diferente.
- Triángulo escaleno: todos los ángulos son diferentes.
- Triángulo rectángulo: un ángulo de 90 grados.
- Fórmula para calcular un ángulo: A = 180° – (B + C).
- Los ángulos exteriores suman 360 grados en un triángulo.
- Uso de la ley de los senos y cosenos para calcular ángulos en triángulos no rectángulos.
¡Dejanos tus comentarios sobre este artículo y no olvides revisar otros temas que podrían interesarte en nuestra web!